GREENHOUSE
MODULE 1
MODULE 2
MODULE 3
R TUTORIAL
CODAPP
HANDOUTS



Using Graphs to Grow the Best Crops

Contributors: Shonda Kuiper, Anna Olsen, Ginger Rowell, DASIL, Shreyas Agrawal' 24











Fun Fact:fun fact icon

Several statistics techniques were originally developed to address agricultural research questions. Click here to read more!




Part 1A: Introduction

Farmers throughout the world face complex challenges. To deliver quality crops to market, farmers need to consider the multiple growing conditions:

  • Soil appropriate to the plants, possibly modified with fertilizer
  • Fresh air, especially carbon dioxide
  • The correct amount of sunlight and water
  • Pesticides, herbicides, and treatments for plant diseases

    • For example, to make a profit, farmers need to decide if they should purchase and apply fertilizer or install an irrigation system. They also need to consider the long-term effects on the environment. A farmer’s challenges do not end with the harvest: changing market conditions may mean that the farmer cannot recover the season’s costs, resulting in a financial loss.

    The Greenhouse Game allows players to grow and sell crops in a virtual greenhouse. It follows the process of planning, planting, growing, harvesting, and selling crops that farmers follow with each growing season. While players can choose any options they like, they are more likely to earn a profit if they use interactive graphs and statistical models to improve their strategies. Here are some key terms each player should know:

  • Yield is the amount of crops produced. It is measured by the number of bushels produced for each plot. In this game, yields reflect actual crop growth in Iowa farmland.
  • A bushel originally was a large basket used to carry crops. For example, a bushel of corn typically weighs about 56 pounds.
  • Water is the amount of water (in inches) that you assign to each plot.
  • A plot is the area of ground where you are planning your seeds. In this Greenhouse game, each test plot represents 1/10th of an acre of land.
  • The game will ask you for a Player ID. You can use any name you like, but this will be on the internet, so do not use a name that will easily identify you.
  • If you are playing this game for a course, your instructor will provide a Group ID so you will be able to compete with everyone in your class.



    • Part 1B: Learning the Greenhouse game

    To learn how to play the game, watch the video below:




    Part 1C: Collecting Data

    The Greenhouse Game can also be an opportunity to consider a variety of research questions, such as what combination of growing conditions would optimize crop yields or profits? Most real-world research questions are much bigger than the resources available to study them, and researchers must limit the scope of their efforts. Similarly, we will start with a simplified question. We will estimate the corn yield based on the amount of water.

    Use the Greenhouse game (below) to collect data on corn yield based on the amount of water:

  • Provide a Player ID (see Figure 1). You may use any name you like: this name will be on the internet, so do not use a name that will easily identify you.
  • Provide a Group ID. If you are playing this game for a course, use the exact Group ID provided by your instructor, which is the same for every person in the class.
  • Select Level 1.
  • On the next screen, note the prices of corn ($30 for each plot) and water ($1 for every inch of water added to each plot).
  • Select corn; enter the six amounts of water as you see in Figure 2; test every combination 5 times; and then select Randomized Play, which assigns each treatment (crop type and water amount) to a randomly selected plot.

    • Figure 1: Settings to start Greenhouse Game for Part 1

    settings to start game

    Figure 2: Settings to generate data for Part 1

    settings to generate data

    Display QR Code, scan it and play on mobile

    NOTE: At this point, do not worry about winning or profits; just carefully follow the instructions below to collect data.

    NOTE: If you are unable to play the game, either try a different browser or go to the game website directly here.

    After you select Randomized Play, you will be able to:

  • Move your cursor over each plot to identify the crop type and the amount of water the plot has received.
  • Click the Harvest button on the right. Then click Sell All to sell your crops. The game will display how much profit you made. Remember the profit for your first season.
  • Click the Data Graph to see the data you collected. Based on this graph, consider which amount of water is best.



    • Part 1D: Exploring Example Data

    Before we analyze the data your class has collected, we will look at an example dataset from someone that already completed this activity. To begin, set Greenhouse App1 to Settings A (at left) and then complete the Creating Graphs questions below.

    Settings A

  • Group ID   sample1
  • X-axis Variable:   Water
  • Y-axis Variable:   Yield
  • Statistical Model:   Linear
  • X-Axis Limits:   (0 - 45)

    • Settings B

  • Group ID   [provided by instructor]
  • X-axis Variable:   Water
  • Y-axis Variable:   Yield
  • Statistical Model:   Linear
  • X-Axis Limits:   (0 - 45)


    • Figure 3: Interpreting the Output

    interpreting the output

    Whenever you select a model in the application on the right, you will also see statistical output. In the output, you can find key summary statistics related to the model you have selected.

    Instructors Note: Go to faculty resources to access student data


    Part 1F: Discussion Questionschallenge icon

    Develop a strategy to optimize your profit when growing corn in Level 1 of the Greenhouse game. Use your statistical knowledge and any analyses you choose to address the following steps:

      1. Provide a graph and briefly explain how the graph helps you determine the amount of water that would give you the highest profits
      2. Play one season of the Greenhouse game again, implementing your strategy:
        a) Provide the same Player ID
        b) Add a “c” at the end of your Group ID. For example, if your Group ID was Stat101S22, now use Stat101S22c
        c) Select Level 1
        d) Select only the corn crop.
        e) Choose any amounts of water and any number of plots.

    After playing one season, submit your Player ID, Income, Expenses, and Profits to your instructor. Compare your profits with those of your fellow students by entering your new Group ID below. Sometimes it can take up to 60 minutes for your class data to show in the app below.

    Part 1G: Get Curious get curious icon

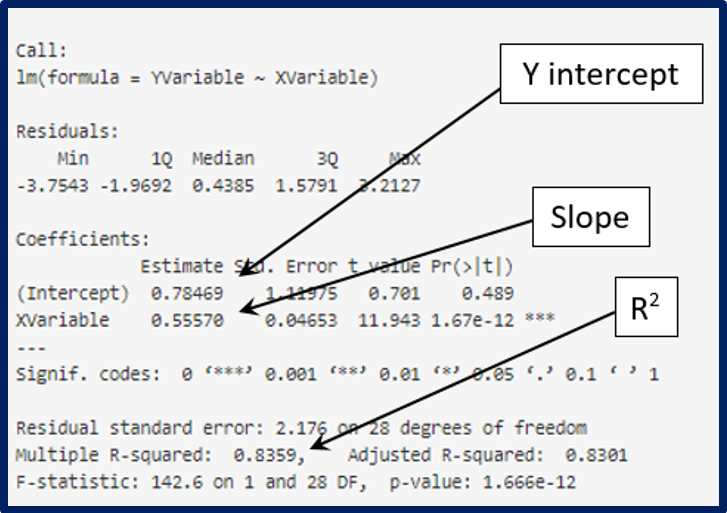
    Evaluating a linear model: Use Settings A in Greenhouse App1

      3. Based on the linear model created in App 1 to address the following questions:
        a) Notice that the yields vary, even when the same amount of water is used. Explain why this should be expected.
        b) Modify the X Axis Limits. When is a linear model a good fit for this data? When is a linear model a poor fit for this data? Briefly explain how you distinguish a good fit from a poor fit.
        c) If modifying the range of the data improves the linear model, would it be appropriate to remove some of our data? Why or why not?

    Evaluating class data: Use Settings B in the Greenhouse App1

      4. Sometimes it can take up to 60 minutes for your class data to show in Greenhouse App1. After your instructor confirms enough class data is available, answer the following questions.
        a) What is the explanatory variable and response variable for this data?
        b) What are the units (what does each point represent)?
        c) Does it look as though all the players followed the instructions in Step 1B? Explain why or why not.
        d) Do the results from your class agree with the sample1 data? Explain why or why not.
        e) Try some different statistical models. Which one looks like it best describes the data?
        f) What conclusions can you draw from this data and the corresponding regression model?
      5. Address the following questions about different ways we could have conducted this study to improve the quality of our data:
        a) Are there better variables to use? For example, what would be the benefits to using Profit or Revenue as the response variable instead of Yield?
        b) What are the benefits to randomizing the amount of water assigned to each plot?
        c) How many plots would need to be tested to convince you that there is a relationship between Water and Yield?
      6. In order to create a meaningful regression model, we should take into account possible confounding variables [variables that the researcher did not include in the study but that might be connected to both the explanatory (independent) variable and the response (dependent) variable]. List at least two potential confounding variables that might get in the way of determining the relationship between Water and Yield.
      7. Go back to the Greenhouse App1, use Group ID = sample1 and Y Variable = Profit, then create a linear model.
        a) Explain why the linear model does not work as well for profit as it did for yield.
        b) Based on this graph, what amount(s) of water should be used to get the most yield?
        c) Create a graph and write a paragraph clearly explaining to a farmer the best strategy to maximize corn profits in one season.
      8. Experiment with making your own graphs in R with this LearnR GreenHouse Tutorial.



    Continue to Part 2


    Data Stories


    NYPD
    Covid-19
    Recidivism
    Brexit

    Stats Games


    Racer
    Greenhouse
    Statistically Grounded
    Psychic

    Questions?


    If you have any questions or comments, please email us at DASIL@grinnell.edu

    Dataspace is supported by the Grinnell College Innovation Fund and was developed by Grinnell College faculty and students. Copyright © 2021. All rights reserved

    This page was last updated on  December 1st  2024.